Hackerrank - Graph Theory - Even Tree

You are given a tree (a simple connected graph with no cycles). The tree has  nodes numbered from  to  and is rooted at node .

Find the maximum number of edges you can remove from the tree to get a forest such that each connected component of the forest contains an even number of nodes.

Input Format

The first line of input contains two integers  and .  is the number of nodes, and  is the number of edges.
The next  lines contain two integers  and  which specifies an edge of the tree.

Note: The tree in the input will be such that it can always be decomposed into components containing an even number of nodes.

Output Format

Print the number of removed edges.

Sample Input

10 9
2 1
3 1
4 3
5 2
6 1
7 2
8 6
9 8
10 8

Sample Output

2

Explanation

On removing edges  and , we can get the desired result.

Original tree:

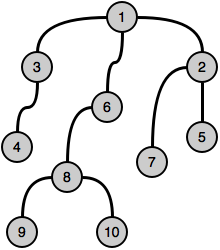
Decomposed tree:

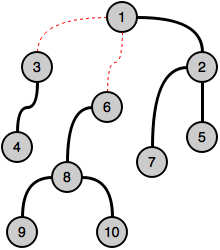
Solution

nb_cuts = 0
v, e = [ int(i) for i in raw_input().split()]
edges = []
for i in range(e):
    edges.append([ int(i) for i in raw_input().split()])

for i in edges:
    loc_edges = list(edges)
    loc_edges.remove(i)
    forest = []
    for j in loc_edges:
        in_tree = False
        for tree in forest:
            loc_tree = list(tree)
            if j[0] in loc_tree:
                in_tree = True
                tree.append(j[1])
                break
            if j[1] in loc_tree:
                in_tree = True
                tree.append(j[0])
                break
        if not in_tree:
            forest.append(list(j))
    even_cut = True
    for tree in forest:
        even_cut = even_cut & (len(tree) %2 ==0)
    if(even_cut):
        nb_cuts+=1
        
print(nb_cuts)